Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Folgen

Grenzwert einer Folge

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Folge

$\displaystyle (a_n) = a_1,a_2,\ldots$

konvergiert gegen einen Grenzwert $ a$ ,

$\displaystyle a=\lim_{n\rightarrow\infty} a_n,$

wenn es zu jedem $ \varepsilon > 0$ ein $ n_\varepsilon$ gibt mit

$\displaystyle \vert a_n -a \vert < \varepsilon $

für alle $ n > n_\varepsilon$ .
\includegraphics[clip,width=0.5\linewidth,height=.3\linewidth]{a_konvergenz_einer_folge.eps}

Man benutzt ebenfalls die Schreibweise $ a_n\rightarrow a$ für eine konvergente Folge. Besitzt $ (a_n)$ keinen Grenzwert, so bezeichnet man die Folge als divergent.

Um das Konvergenz-Kriterium

$\displaystyle \vert a_n - a\vert < \varepsilon \;$   für$\displaystyle \; n > n_{\varepsilon} $

nachzuweisen, kann man zunächst den Ausdruck $ \vert a_n - a\vert$ durch Abschätzung nach oben vereinfachen und dann die so gewonnene Ungleichung nach $ n$ auflösen.

Wendet man dies beispielsweise für die Folge

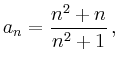
$\displaystyle a_n = \dfrac{n^2+n}{n^2+1}\,, $

die den Grenzwert $ a=1$ besitzt, an, ist eine mögliche Abschätzung

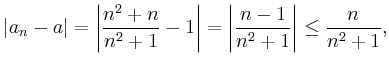
$\displaystyle \vert a_n - a\vert = \left\vert \frac{n^2+n}{n^2+1} - 1 \right\vert = \left\vert \frac{n-1}{n^2+1} \right\vert \leq \frac{n}{n^2+1}, $

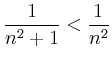da $ \vert n-1\vert \le n$ für alle $ n\ge 0$. Ausserdem ist $ n^2+1 > n^2$ und damit auch $ \dfrac{1}{n^2+1} < \dfrac{1}{n^2}$. Also folgt daraus

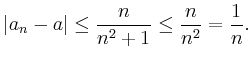
$\displaystyle \vert a_n - a\vert \leq \frac{n}{n^2+1} \leq \frac{n}{n^2} = \frac{1}{n}. $

Damit 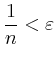$ \dfrac{1}{n} < \varepsilon$ ist, muss 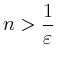$ n > \dfrac{1}{\varepsilon}$ sein. Wählt man nun $ n_\varepsilon$ als eine natürliche Zahl größer als $ \dfrac{1}{\varepsilon}$, dann gilt für alle $ \varepsilon >0$ und alle $ n > n_{\varepsilon}$

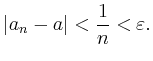
$\displaystyle \vert a_n - a\vert < \frac{1}{n} < \varepsilon. $

(Autoren: Höllig/Kreitz)
Die Folge

$\displaystyle 1,q,q^2,\ldots $

besitzt für $ \vert q\vert<1$ den Grenzwert 0 und divergiert für $ \vert q\vert>1$ oder $ q=-1$ .
(Autor: Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009