Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Folgen

Monotone Konvergenz

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Folge $ (a_n)$ heißt monoton wachsend bzw. monoton fallend, wenn $ a_{n+1} \ge a_n$ bzw. $ a_{n+1} \le a_n$ für alle $ n$. Sie heißt streng monoton wachsend bzw. streng monoton fallend, wenn $ a_{n+1} > a_n$ bzw. $ a_{n+1} < a_n$ für alle $ n$.

\includegraphics[clip,width=.6\linewidth,height=.3\linewidth]{a_monotone_konvergenz.eps}

Eine beschränkte, für $ n > n_0$ monoton wachsende oder fallende Folge $ (a_n)$ ist konvergent. Der Grenzwert ist das Supremum bzw. Infimum der Folgenelemente $ a_n$, $ n > n_0$.

Für eine monoton wachsende Folge folgt mit der Definition des Supremums, dass für alle $ \varepsilon>0$ ein $ n_{\varepsilon}$ existiert.

$\displaystyle a-\varepsilon < a_{n_{\varepsilon}} \leq a = \sup_{n>n_0}a_n $

Aufgrund der Monotonie ist

$\displaystyle a-\varepsilon < a_{n_{\varepsilon}} \leq a_n \leq a$   , für $\displaystyle n > {n_{\varepsilon}}\; , $

also $ a_n \rightarrow a$ .

Für monoton fallende Folgen argumentiert man analog.

(Autoren: App/Höllig )
Die Konvergenz der Folge

$\displaystyle a_n = (1 + 1/n)^n,\quad n = 0, 1, ..., $

gegen die Eulersche Zahl $ e$ kann mit dem Satz über monotone Konvergenz gezeigt werden. Beide Voraussetzungen können mit Hilfe des binomischen Lehrsatzes bewiesen werden.

(i) Beschränktheit: Aus

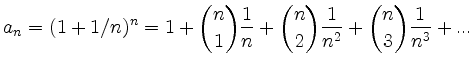
$\displaystyle a_n = (1+1/n)^n = 1 + {n \choose 1} \frac{1}{n} + {n \choose 2}\frac{1}{n^2} + {n \choose 3}\frac{1}{n^3} + ... $

und

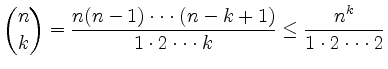
$\displaystyle {n \choose k} = \frac{n(n-1)\cdot\cdot\cdot(n-k+1)}{1\cdot2\cdot\cdot\cdot k} \leq \frac{n^k}{1\cdot2\cdot\cdot\cdot2} $

folgt

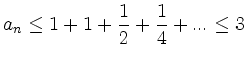
$\displaystyle a_n \leq 1 + 1 + \frac{1}{2} + \frac{1}{4} + ... \leq 3 $

(ii) Monotonie: Man berechnet $ a_{n+1}$ ebenfalls mit dem binomischen Lehrsatz:

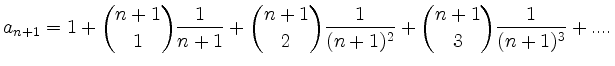
$\displaystyle a_{n+1} = 1 + {n+1 \choose 1} \frac{1}{n+1} + {n+1 \choose 2}\frac{1}{(n+1)^2} + {n+1 \choose 3}\frac{1}{(n+1)^3} + ... . $

Vergleicht man mit der Darstellung von $ a_n$ in (i), so stellt man fest, dass die entsprechenden Terme größer sind:
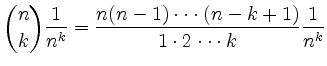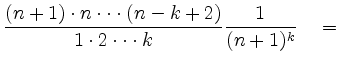$\displaystyle {n \choose k}\frac{1}{n^k} = \frac{n(n-1)\cdot\cdot\cdot(n-k+1)}{1\cdot2\cdot\cdot\cdot k}\frac{1}{n^k}$ $\displaystyle \leq$ $\displaystyle \frac{(n+1)\cdot n\cdot\cdot\cdot(n-k+2)}{1\cdot2\cdot\cdot\cdot k}\frac{1}{(n+1)^k}\quad=$  
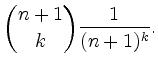  $\displaystyle =$ $\displaystyle {n+1 \choose k}\frac{1}{(n+1)^k}.$  

Dies folgt aus der Ungleichung

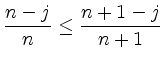
$\displaystyle \frac{n-j}{n} \leq \frac{n+1-j}{n+1} $

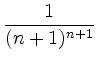für die einzelnen Faktoren. Da die Summe für $ a_{n+1}$ noch den Term $ \displaystyle \frac{1}{(n+1)^{n+1}}$ enthält folgt

$\displaystyle a_n < a_{n+1}.$

(Autor: Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009