Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM I - Folgen, Reihen, stetige Funktionen

Reihen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Begriff.

Sei $ \mbox{$m\in\mathbb{Z}$}$, sei $ \mbox{$(a_n)_{n\geq m}$}$ eine komplexe Folge. Die daraus gebildete Folge

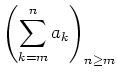
$ \mbox{$\displaystyle \left(\sum_{k = m}^n a_k\right)_{n\geq m} $}$
heißt Reihe. Deren Folgenglieder $ \mbox{$\sum_{k = m}^n a_k$}$ werden auch als Partialsummen der Reihe bezeichnet. Von den Gliedern $ \mbox{$a_n$}$ spricht man hingegen als von den Summanden der Reihe.

Falls existent, so wird ihr Grenzwert als

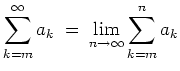
$ \mbox{$\displaystyle \sum_{k = m}^\infty a_k \; =\: \lim_{n\to\infty} \sum_{k = m}^n a_k $}$
bezeichnet, und wir sprechen von einer konvergenten Reihe. Falls der Grenzwert nicht existiert, so heißt die Reihe divergent. Gelegentlich bezeichnet man mit $ \mbox{$\sum_{k = m}^\infty a_k$}$ auch die zugrundeliegende Reihe selbst.

Die Reihe $ \mbox{$\sum_{k = m}^\infty a_k$}$ heiße absolut konvergent, falls die Reihe der Beträge $ \mbox{$\sum_{k = m}^\infty \vert a_k\vert$}$ konvergiert. Eine absolut konvergente Reihe ist insbesondere konvergent. Umgekehrt ist z.B. $ \mbox{$\sum_{k = 1}^\infty (-1)^k k^{-1}$}$ konvergent, aber nicht absolut konvergent. Bei einer absolut konvergenten Reihe dürfen die Summanden beliebig vertauscht werden.

Falls keine Mißverständnisse zu befürchten sind, schreiben wir auch $ \mbox{$\sum_{k = m}^\infty a_k =: \sum_k a_k$}$.

Regeln.

Seien $ \mbox{$\sum_k a_k\;$}$, $ \mbox{$\sum_k b_k$}$ konvergente Reihen, seien $ \mbox{$\lambda,\mu\in\mathbb{C}$}$.

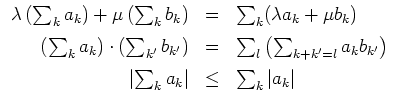
$ \mbox{$\displaystyle \begin{array}{rcl} \lambda\left(\sum_k a_k\right) + \mu\... ...eft\vert\sum_k a_k\right\vert & \leq & \sum_k \vert a_k\vert \\ \end{array}$}$
Für die Multiplikationsregel, das sogenannte Cauchyprodukt, muß dabei wenigstens eine der beiden Reihen der linken Seite absolut konvergent sein.

Kriterien.

Sei $ \mbox{$\sum_k a_k$}$ eine Reihe mit komplexen Summanden.

Nullfolge. Wenn die Reihe $ \mbox{$\sum_k a_k$}$ konvergiert, dann ist die Folge ihrer Summanden $ \mbox{$(a_k)_k$}$ eine Nullfolge. Die Umkehrung gilt nicht, wie man etwa an der divergenten harmonischen Reihe $ \mbox{$\sum_{k = 1}^\infty k^{-1}$}$ erkennt.

Leibnizkriterium. Ist $ \mbox{$(a_n)_n$}$ eine monoton fallende Nullfolge mit Gliedern in $ \mbox{$\mathbb{R}_{\geq 0}$}$, so konvergiert

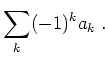
$ \mbox{$\displaystyle \sum_k (-1)^k a_k\; . $}$

Dirichletkriterium. Sei die Folge der Partialsummen $ \mbox{$(\sum_{k=k_0}^n a_k)_n$}$ beschränkt, und sei $ \mbox{$(b_k)_k$}$ eine reelle monotone Nullfolge. Dann konvergiert die Reihe $ \mbox{$\sum_k a_k b_k$}$.

Majorantenkriterium. Gibt es eine konvergente Reihe $ \mbox{$\sum_k b_k$}$ mit Summanden in $ \mbox{$\mathbb{R}_{\geq 0}$}$ und ist $ \mbox{$\vert a_k\vert \leq b_k$}$ stets, so ist $ \mbox{$\sum_k a_k$}$ absolut konvergent.

Quotientenkriterium. Sei $ \mbox{$a_k\neq 0$}$ stets (lasse ggf. die Reihe später beginnen).

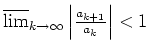  1. Ist $ \mbox{$\overline {\lim}_{k\to\infty} \left\vert\frac{a_{k+1}}{a_k}\right\vert < 1$}$, so ist $ \mbox{$\sum_k a_k$}$ absolut konvergent.
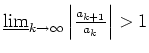  2. Ist $ \mbox{$\underline {\lim}_{k\to\infty} \left\vert\frac{a_{k+1}}{a_k}\right\vert > 1$}$, so ist $ \mbox{$\sum_k a_k$}$ divergent.

Wir erinnern daran, daß $ \mbox{$\overline {\lim}_{k\to\infty} = \underline {\lim}_{k\to\infty} = \lim_{k\to\infty}$}$, falls letzterer existiert. Ist dieser gleich $ \mbox{$1$}$, so hilft das Quotientenkriterium nicht.

Wurzelkriterium.

  1. Ist $ \mbox{$\overline {\lim}_{k\to\infty} \sqrt[k]{\vert a_k\vert} < 1$}$, so ist $ \mbox{$\sum_k a_k$}$ absolut konvergent.
  2. Ist $ \mbox{$\overline {\lim}_{k\to\infty} \sqrt[k]{\vert a_k\vert} > 1$}$, so ist $ \mbox{$\sum_k a_k$}$ divergent.

Ist $ \mbox{$\overline {\lim}_{k\to\infty} \sqrt[k]{\vert a_k\vert} = 1$}$, so hilft das Wurzelkriterium nicht.

Cauchysches Verdichtungskriterium.

Sei die Folge der Summanden $ \mbox{$(a_k)_k$}$ positiv und monoton fallend. Die Reihe $ \mbox{$\sum_k a_k$}$ konvergiert genau dann, wenn die verdichtete Reihe $ \mbox{$\sum_k 2^k a_{2^k}$}$ konvergiert.

(Autoren: Künzer/Martin/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 18.6.2004