Mathematik-Online-Kurs: Repetitorium HM I-Folgen, Reihen, stetige Funktionen-Funktionsgrenzwerte

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Repetitorium HM I - Folgen, Reihen, stetige Funktionen
	Funktionsgrenzwerte

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Der Abschluß einer Menge.

Sei $\mbox{$D\subseteq \mathbb{C}$}$ eine Teilmenge. Ein Punkt $\mbox{$z_0\in\mathbb{C}$}$ heiße Berührpunkt von $\mbox{$D$}$ , falls jede $\mbox{$\varepsilon $}$ -Umgebung $\mbox{$B_\varepsilon (z_0) = \{ z\in\mathbb{C}\; \vert\; \vert z - z_0\vert < \varepsilon \}$}$ mit $\mbox{$D$}$ nichtleeren Schnitt hat. Insbesondere sind alle Punkte in $\mbox{$D$}$ auch Berührpunkte von $\mbox{$D$}$ .

Die Menge aller Berührpunkte wird als Abschluß von $\mbox{$D$}$ bezeichnet, und

$\mbox{$\displaystyle \bar{D} \; :=\; \{ z\in\mathbb{C}\; \vert\; B_\varepsilon (z) \cap D\neq\emptyset \;\;\forall\,\varepsilon > 0\} $}$

geschrieben. Dies ist zugleich die Menge der Punkte $\mbox{$z$}$ in $\mbox{$\mathbb{C}$}$ , für die eine Folge mit Folgengliedern in $\mbox{$D$}$ existiert, welche gegen $\mbox{$z$}$ konvergiert.

Ist $\mbox{$D\subseteq \mathbb{R}$}$ , dann ist auch $\mbox{$\bar{D}\subseteq \mathbb{R}$}$ .

Begriff.

Sei $\mbox{$D\subseteq \mathbb{C}$}$ eine Teilmenge, und sei $\mbox{$f:D\longrightarrow \mathbb{C}$}$ eine Funktion. (Dies deckt wegen $\mbox{$\mathbb{R}\subseteq \mathbb{C}$}$ auch den Fall reeller Funktionen ab.)

Es heißt $\mbox{$y_0\in\mathbb{C}$}$ der Grenzwert von $\mbox{$f$}$ an der Stelle $\mbox{$x_0\in\bar{D}$}$ , falls es für alle $\mbox{$\varepsilon > 0$}$ ein $\mbox{$\delta > 0$}$ gibt mit

$\mbox{$\displaystyle \vert f(x) - y_0\vert \; < \; \varepsilon $}$

für alle $\mbox{$x\in D$}$ mit

$\mbox{$\displaystyle \vert x - x_0\vert\; < \; \delta\; . $}$

In anderen Worten, für alle $\mbox{$\varepsilon > 0$}$ gibt es ein $\mbox{$\delta > 0$}$ so, daß $\mbox{$f(B_\delta(x_0)\cap D) \subseteq B_\varepsilon (y_0)$}$ .

Existiert der Grenzwert $\mbox{$y_0$}$ bei $\mbox{$x_0$}$ , dann sagen wir, $\mbox{$f$}$ konvergiert an der Stelle $\mbox{$x_0$}$ gegen $\mbox{$y_0$}$ und schreiben

$\mbox{$\displaystyle \lim_{x\to x_0} f(x) \; =\; \lim_{x\to x_0,\; x\in D} f(x) \; := \; y_0\; . $}$

(Manche Autoren setzen auch $\mbox{$\lim_{x\to x_0} f(x) \; = \lim_{x\to x_0,\; x\in D\backslash \{ x_0\}} f(x)$}$ , unter weiteren Voraussetzungen an $\mbox{$x_0$}$ .)

Ist $\mbox{$D\subseteq \mathbb{R}$}$ , so schreibt man

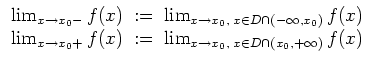
$\mbox{$\displaystyle \begin{array}{rcl} \lim_{x\to x_0-} f(x) \; :=\; \lim_{x... ...(x) \; :=\; \lim_{x\to x_0,\; x\in D\cap (x_0,+\infty)} f(x) \\ \end{array}$}$

für den links- bzw. rechtsseitigen Grenzwert bei $\mbox{$x_0$}$ (vorausgesetzt, es ist $\mbox{$D\cap (-\infty)\neq\emptyset $}$ bzw. $\mbox{$D\cap (x_0,+\infty)\neq\emptyset $}$ ).

Unendlich.

Sei $\mbox{$D\subseteq \mathbb{R}$}$ , sei $\mbox{$f:D\longrightarrow \mathbb{R}$}$ eine Funktion, und sei $\mbox{$x_0\in\bar{D}$}$ .

Im folgenden bezeichnen die Klammern ( ) und [ ] die jeweiligen Fälle.

Wir schreiben $\mbox{$\lim_{x\to x_0} f(x) = +\infty \;\; (-\infty)$}$ , falls für alle $\mbox{$e > 0$}$ ein $\mbox{$\delta > 0$}$ existiert mit

$\mbox{$\displaystyle f(x) \; >\; e \;\; (\; <\; -e\; ) $}$

für alle $\mbox{$x\in D$}$ mit

$\mbox{$\displaystyle \vert x - x_0\vert\; < \; \delta\; . $}$

Wir schreiben $\mbox{$\lim_{x\to +\infty} f(x) = y_0$}$ [ $\mbox{$\lim_{x\to -\infty} f(x) = y_0$}$ ], falls für alle $\mbox{$\varepsilon > 0$}$ ein $\mbox{$d > 0$}$ existiert mit

$\mbox{$\displaystyle \vert f(x) - y_0\vert \; < \; \varepsilon $}$

für alle $\mbox{$x\in D$}$ mit

$\mbox{$\displaystyle x \; > \; d \;\; {[\; < \; -d\; ]} \; . $}$

Dies hat nur einen Sinn, falls $\mbox{$D$}$ nach oben [nach unten] unbeschränkt ist.

Wir schreiben $\mbox{$\lim_{x\to +\infty} f(x) = +\infty$}$ ( $\mbox{$-\infty$}$ ) [ $\mbox{$\lim_{x\to -\infty} f(x) = +\infty$}$ ( $\mbox{$-\infty$}$ )], falls für alle $\mbox{$e > 0$}$ ein $\mbox{$d > 0$}$ existiert mit

$\mbox{$\displaystyle f(x) \; >\; e \;\; (\; <\; -e\; ) $}$

für alle $\mbox{$x\in D$}$ mit

$\mbox{$\displaystyle x \; > \; d \;\; {[\; < \; -d\; ]} \; . $}$

Auch dies hat nur einen Sinn, falls $\mbox{$D$}$ nach oben [nach unten] unbeschränkt ist.

In all diesen Fällen heißt $\mbox{$f$}$ an der betrachteten Stelle bestimmt divergent.

Folgenkriterium.

Sei $\mbox{$D\subseteq \mathbb{C}$}$ eine Teilmenge, sei $\mbox{$f:D\longrightarrow \mathbb{C}$}$ eine Funktion, sei $\mbox{$x_0\in\bar{D}$}$ , und sei $\mbox{$y_0\in\mathbb{C}$}$ .

Es ist $\mbox{$\lim_{x\to x_0} f(x) = y_0$}$ genau dann, wenn für jede Folge $\mbox{$(x_n)_{n\geq 1}$}$ mit $\mbox{$x_n\in D$}$ und $\mbox{$x_n\to x_0$}$ auch $\mbox{$f(x_n)\to y_0$}$ geht für $\mbox{$n\to\infty$}$ .

Variante.

Sei $\mbox{$D\subseteq \mathbb{R}$}$ eine Teilmenge, sei $\mbox{$f:D\longrightarrow \mathbb{R}$}$ eine Funktion, sei $\mbox{$x_0\in\bar{D}$}$ , und sei $\mbox{$y_0\in\hat {\mathbb{R}}$}$ . Ist $\mbox{$D$}$ nach oben [unten] unbeschränkt, so lassen wir auch noch $\mbox{$x_0 = +\infty$}$ [ $\mbox{$x_0 = -\infty$}$ ] zu.

Grenzwertregeln.

Elementare Regeln. Sei $\mbox{$D\subseteq \mathbb{C}$}$ eine Teilmenge, seien $\mbox{$f,g:D\longrightarrow \mathbb{C}$}$ Funktionen, die an der Stelle $\mbox{$x_0\in\bar{D}$}$ konvergieren, und seien $\mbox{$\lambda,\mu\in\mathbb{C}$}$ . Es gelten folgende Regeln.

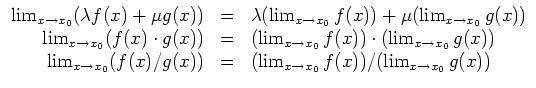
$\mbox{$\displaystyle \begin{array}{rcl} \lim_{x\to x_0} (\lambda f(x) + \mu g... ... / g(x)) & = & (\lim_{x\to x_0} f(x))/(\lim_{x\to x_0} g(x)) \\ \end{array}$}$

Für die Divisionsregel brauchen wir $\mbox{$g(x)\neq 0$}$ für $\mbox{$x\in D$}$ (ggf. nach Verkleinerung von $\mbox{$D$}$ ) und auch $\mbox{$\lim_{x\to x_0} g(x)\neq 0$}$ .

Zweiseitige Betrachtung. Sei $\mbox{$D\subseteq \mathbb{R}$}$ eine Teilmenge, sei $\mbox{$f:D\longrightarrow \mathbb{C}$}$ eine Funktion, und sei $\mbox{$x_0\in\bar{D}$}$ . Falls links- und rechtsseitiger Grenzwert bei $\mbox{$x_0$}$ existieren und übereinstimmen, so konvergiert $\mbox{$f$}$ in $\mbox{$x_0$}$ , und es ist

$\mbox{$\displaystyle \lim_{x\to x_0} f(x) \; =\; \lim_{x\to x_0-} f(x)\; =\; \lim_{x\to x_0+} f(x)\; . $}$

Und umgekehrt, wenn der Grenzwert bei $\mbox{$x_0$}$ existiert, so existiert er auch links- und rechtsseitig, und die Grenzwerte stimmen überein.

Verkettungsregel. Seien $\mbox{$f$}$ und $\mbox{$g$}$ komplexwertige Funktionen, sei $\mbox{$\lim_{z\to z_0} f(z) = w_0$}$ , und sei $\mbox{$\lim_{w\to w_0} g(w) = v_0$}$ . Dann ist $\mbox{$\lim_{z\to z_0} g(f(z)) = v_0$}$ . Analoge Regeln gelten bei $\mbox{$\pm\infty$}$ .

(Autoren: Künzer/Martin/Nebe)

Beispiele

Aufgaben

automatisch erstellt am 18.6.2004