Die Partitionen von 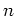 stehen in Bijektion zu den Konjugiertenklassen von
stehen in Bijektion zu den Konjugiertenklassen von 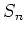 .
.
Die Bijektion ist dadurch gegeben, dass man einer Partition
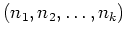 eine Permutation
eine Permutation
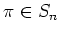 zuordnet, die aus
zuordnet, die aus 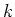 paarweise disjunkten Zykeln der Länge
paarweise disjunkten Zykeln der Länge 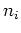 besteht.
besteht.
Die Ordnung eines Repräsentanten 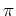 der zur Partition
der zur Partition
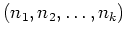 gehörenden Konjugiertenklasse ist gegeben durch
gehörenden Konjugiertenklasse ist gegeben durch
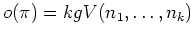 .
.
(Autoren: Höfert/Kimmerle)
Die Konjugierenklassen von 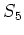 sind gegeben durch
sind gegeben durch
| |
Repräsentant 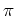 der der |
|
| Partition |
Konjugiertenklasse von 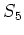 |
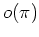 |
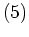 |
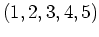 |
5 |
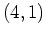 |
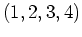 |
4 |
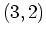 |
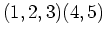 |
6 |
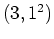 |
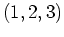 |
3 |
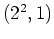 |
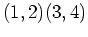 |
2 |
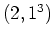 |
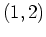 |
2 |
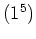 |
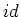 |
1 |
(Autoren: Höfert/Kimmerle)
| |
automatisch erstellt
am 14.11.2008 |


![]() eine Permutation
eine Permutation
![]() zuordnet, die aus
zuordnet, die aus ![]() paarweise disjunkten Zykeln der Länge
paarweise disjunkten Zykeln der Länge ![]() besteht.
besteht.
![]() der zur Partition
der zur Partition
![]() gehörenden Konjugiertenklasse ist gegeben durch
gehörenden Konjugiertenklasse ist gegeben durch
![]() .
.