Mathematik-Online-Kurs: Gruppentheorie-Permutationsgruppen-Der Satz von Sylow-Satz von Sylow; Sylowgruppen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Gruppentheorie - Permutationsgruppen - Der Satz von Sylow
	Satz von Sylow; Sylowgruppen

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Sei

eine endliche Gruppe,

eine Primzahl und $\alpha \in \mathbb{N}_0$ mit $\vert G\vert=p^\alpha \cdot n$ , wobei $\textrm{ggT}(p,n)=1$ .

(a)

Existenz von Sylowgruppen

besitzt mindestens eine Untergruppe der Ordnung $p^\alpha$ .

Die Untergruppen dieser Ordnung nennt man Sylowgruppen von . Mit bezeichnet man die Menge der Sylowgruppen von .

(b)

Eindeutigkeit von Sylowgruppen
Seien $U,V \in Syl_p(G)$ . Dann gibt es ein $g \in G$ mit

Verschiedene Sylowgruppen sind also zueinander konjugiert. Somit sind die Sylowgruppen bis auf einen inneren Automorphismus eindeutig bestimmt.

Ist eine Untergruppe von , d.h. eine Untergruppe mit $\vert W\vert=p^b$ , dann existiert eine Sylowgruppe von mit $W \leq S$ .

(c)

Anzahl von Sylowgruppen
$\vert Syl_p(G)\vert \equiv 1 \mod p$ und $\vert Syl_p(G)\vert=\vert G:N_G(U)\vert$ für $U \in Syl_p(G)\vert$ .

Bemerkungen:

Gibt es zu einer Primzahl genau eine Sylowgruppe so ist diese normal in .
Teilt die Gruppenordnung nicht, so ist die Sylowgruppe trivial.

(Autoren: Höfert/Kimmerle)

Für $p \nmid \vert G\vert$ ist der Satz trivialerweise richtig. Ebenso für Gruppen von Primzahlpotenzordnung.

a)

Zunächst werden die folgenden Behauptungen bewiesen.

Behauptung 1: Ist eine abelsche Gruppe mit $\vert G\vert=n$ und teilt , dann existiert ein Element $x \in G$ mit .

Beweis von Behauptung 1: Die Behauptung ist richtig, wenn zyklisch ist, denn für $G=\langle t \rangle$ und gilt und $t^s \neq 1$ . Somit ist ein Element der Ordnung .
Sei nun $\vert G\vert=n$ und ein minimales Gegenbeispiel. Wegen der Minimalität von besitzt dann jede echte Untergruppe von Ordnung (d.h. $p \nmid \vert U\vert$ ). Sei . Wegen $p \mid \vert G\vert$ folgt $p \mid \vert U\vert$ oder $p \mid \vert G/U\vert$ . Also gilt $p \mid \vert G/U\vert$ und hat ein Element der Ordnung , wobei das Bild von $x \in G$ unter der Faktorabbildung $\kappa: G \longrightarrow G/U$ . Sei $Z=\langle x \rangle$ , dann ist $\kappa(Z)=\langle xU \rangle \cong C_p$ eine zyklische Gruppe der Ordnung und wegen $Z/\left(Ker(\kappa) \cap Z \right) \cong C_p$ folgt, dass die Ordnung von teilt. Wiederum wegen der Minimalität von folgt dann, dass ein Element der Ordnung besitzt, und damit auch . Also gibt es kein minimales Gebenbeispiel.

Behauptung 2: Sei ein kleinstes Gegenbeispiel zu Teil a) des Sylowsatzes, dann gilt $p \mid \vert Z(G)\vert$ .

Beweis von Behauptung 2: Man kann als nicht-abelsch annehmen. Des Weiteren gilt $p \mid \vert G\vert$ , da der Satz für $p \nmid \vert G\vert$ wahr ist. Für die Operation von auf sich selbst durch Konjugation gilt die Klassengleichung

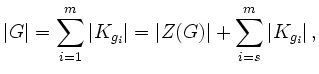
$\displaystyle \vert G\vert= \sum \limits_{i=1}^m \vert K_{g_i}\vert= \vert Z(G)\vert+\sum \limits_{i=s}^m \vert K_{g_i}\vert \,,$

wobei $K_{g_i}$ die Konjugiertenklasse von

mit dem Repräsentanten

ist, $\{g_1, \ldots, g_{s-1}\}$ ein Repräsentantensystem der Klassen von Länge

und $\{g_s, \ldots, g_{m}\}$ ein Repräsentantensystem der Klassen von Länge größer als

Angenommen es existiert ein Index mit $(p,\vert K_{g_i}\vert)=1$ (für $s \leq j \leq m$ ). Nach dem Bahnenlemma gilt

$\displaystyle \vert K_{g_j}\vert=\vert G/C_G(g_j)\vert\,.$

Wegen $(p,\vert K_{g_i}\vert)=1$ folgt dann, dass $p^\alpha \nmid \vert G(C_G(g_j)\vert$ , also gilt $p^\alpha \mid \vert C_G(g_j)\vert$ . Da

ein kleinstes Gegenbeispiel und $\vert C_G(g_j)\vert < \vert G\vert$ ist folgt, dass

Sylowgruppen der Ordnung $p^\alpha$ hat. Damit besitzt aber auch

solche Untergruppen und ist daher kein Gegenbeispiel. Also folgt $p \mid \vert K_{g_j}\vert$ für alle $j\geq s$ , und damit $p \mid \vert Z(G)\vert$ .

Behauptung 3: Sei $\varphi: G \longrightarrow H$ ein surjektiver Homomorphismus. Ist $U \leq H$ , dann ist $\varphi(U) \leq G$ . Ist endlich, dann gilt $\vert\varphi^{-1}(U)\vert=\vert U\vert \cdot \vert Ker (\varphi)\vert$ .

Beweis von Behauptung 3: Sind $x,y \in \varphi^{-1}(U)$ , dann ist $\varphi(xy^{-1})=\varphi(x)\varphi(y)^{-1}$ . Damit ist $xy^{-1}\in \varphi^{-1}(U)$ und nach dem Untergruppenkriterium ist $\varphi^{-1}(U)\leq G$ .

Man beachte, dass $\varphi^{-1} (U)\supseteq Ker \varphi$ ist, denn $\varphi(Ker(\varphi))=1 \leq U$ und $\varphi(\varphi^{-1}(U))=U$ , da $\varphi$ surjektiv. Nach dem Homomorphisatz ist $\varphi^{-1}(U)/Ker(\varphi) \cong U$ und damit

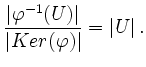
$\displaystyle \frac{\vert\varphi^{-1}(U)\vert}{\vert Ker(\varphi)\vert}=\vert U\vert \,.$

Beweisabschluss von Teil a): Sei ein kleinster Verbrecher. Nach Behauptung 2 gilt $Z(G) \neq 1$ und $p \mid \vert Z(G)\vert$ . Nach Behauptung 1 existiert ein Element $x\in Z(G)$ mit . Damit folgt, dass $Z(G) \cong C_p$ zyklisch ist und $\langle x \rangle \vartriangleleft G$ , da zentral. Man beachte, dass $\langle x \rangle \neq G$ gilt, da keine Gruppe ist. Betrachte nun die Abbildung

$\displaystyle \varphi \ : \ g \longrightarrow G/ \langle x \rangle \,.$

Nach Voraussetzung ist $G/\langle x \rangle$ kein Verbrecher, und es gilt

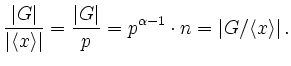
$\displaystyle \displaystyle{ \frac{\vert G\vert}{\vert\langle x \rangle\vert} =... ...c{\vert G\vert}{p}=p^{\alpha-1} \cdot n = \vert G/ \langle x \rangle\vert} \,.$

Es existiert also eine Sylowgruppe

von $G/\langle x \rangle$ mit $\vert U\vert=p^{\alpha-1}$ . Nach Behauptung 3 ist

$\displaystyle \varphi^{-1}(U)=p \cdot p^{\alpha-1}=p^{\alpha} \,.$

Damit hat

eine

Sylowgruppe und es existiert kein kleinster Verbrecher. Teil a) ist damit bewiesen.

b)

Sei

eine

Untergruppe von

und $P \in Syl_p(G)=M$ . Setze $\widetilde{M}= \{ P^g \ ; \ g\in G \}$ . Nach dem Bahnenlemma gilt $\vert\widetilde{M}\vert=\vert G/N_G(P)\vert$ . Wegen $\vert P\vert=p^\alpha$ it

kein Teiler von $\vert\widetilde{M}\vert$ . Andererseits operiert

via Konjugation auf $\widetilde{M}$ . Da

eine

Gruppe ist besitzen alle Bahnen der

Operation Längen der Form $p^\gamma$ mit $\gamma \in {\mathbb{N}}_0$ .

Angenommen es ist $\gamma \geq 1$ , dann ist $\vert\widetilde{M}\vert \equiv 0 \mod p$ , im Widerspruch zu $p \nmid \vert\widetilde{M}\vert$ . Also existiert ein $\widetilde{P}=P^{g_0}$ mit $\widetilde{P}^x= \widetilde{P}$ für alle $x \in W$ und es ist $W \leq N_G(\widetilde{P})$ . Weiter ist $\widetilde{P} \unlhd N_G(\widetilde{P})$ . Betrachte nun $\widetilde{P} \cdot W$ . Dann ist $\widetilde{P} \cdot W$ eine Untergruppe von $N_G(\widetilde{P})$ , da $\widetilde{P} \unlhd N_G(\widetilde{P})$ . Nach dem Isomorphisatz folgt $\widetilde{P} \cdot W=\widetilde{P}$ und damit $W \leq \widetilde{P}$ .