Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Darstellungen von Gruppen - Grundlagen zur Darstellungstheorie

Hermitisches G-invariantes Skalarprodukt

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Es sei $ (,)_0$ ein hermitisches Skalarprodukt auf dem Vektorraum $ V$. Zu einer linearen Darstellung $ r$ einer endlichen Gruppe $ G$ auf $ V$ definiert man ein $ G-$invariantes hermitisches Skalarprodukt $ (,)$ auf $ V$ wie folgt:

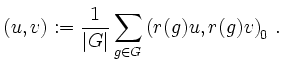
$\displaystyle (u,v):= \frac{1}{\vert G\vert} \sum_{g \in G} \left(r(g)u,r(g)v \right)_0 \,. $

Bemerkung: Auf einem endlich-dimensionalen $ \mathbb{C}$-Vektorraum existiert immer ein hermitisches Skalarprodukt.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008