
Mathematik-Online-Kurs: Repetitorium HM I - Integration

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM I - Integration | |
Das Riemann-Integral und der Hauptsatz |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Der Integralbegriff.
Seien
![]() , sei
, sei
![]() . Sei
. Sei
![]() eine beschränkte Funktion. Zum Beispiel ist dies erfüllt, falls
eine beschränkte Funktion. Zum Beispiel ist dies erfüllt, falls
![]() stetig ist.
stetig ist.
Sei eine Unterteilung
![]() von
von
![]() gewählt. Der Flächeninhalt
zwischen
gewählt. Der Flächeninhalt
zwischen
![]() -Achse und Funktionsgraph (negativ genommen unter der
-Achse und Funktionsgraph (negativ genommen unter der
![]() -Achse) wird von oben angenähert durch die
Obersumme
-Achse) wird von oben angenähert durch die
Obersumme
![$ \mbox{$\displaystyle
\Sigma^\bullet(f,\underline {x}) \; :=\; \sum_{i = 1}^n (x_i - x_{i-1})\sup f([x_{i-1},x_i])
$}$](/inhalt/aussage/aussage1165/img8.png)
![$ \mbox{$\displaystyle
\Sigma_\bullet(f,\underline {x}) \; :=\; \sum_{i = 1}^n (x_i - x_{i-1})\inf f([x_{i-1},x_i])\; .
$}$](/inhalt/aussage/aussage1165/img9.png)
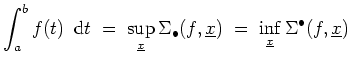
Zum Beispiel ist
![]() integrierbar, falls
integrierbar, falls
![]() stetig ist, oder auch, falls
stetig ist, oder auch, falls
![]() monoton wachsend oder monoton fallend ist.
monoton wachsend oder monoton fallend ist.
Anschaulich beziffert das Integral also den Flächeninhalt zwischen
![]() -Achse und Funktionsgraph, wobei die Teile unterhalb
der
-Achse und Funktionsgraph, wobei die Teile unterhalb
der
![]() -Achse negativ zu nehmen sind.
-Achse negativ zu nehmen sind.
Man setzt noch
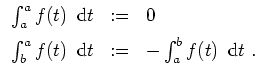
Zwischensummen.
Ist
![]() ein Tupel von Zwischenpunkten der Unterteilung
ein Tupel von Zwischenpunkten der Unterteilung
![]() , wofür wir verlangen, daß
, wofür wir verlangen, daß
![]() für
für
![]() , so erhält man eine Zwischensumme
, so erhält man eine Zwischensumme
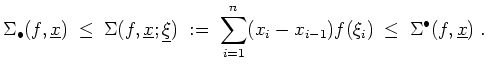
Sei
![]() eine Folge von Unterteilungen mit
eine Folge von Unterteilungen mit
![]() für
für
![]() , und sei
, und sei
![]() jeweils ein Tupel von Zwischenpunkten von
jeweils ein Tupel von Zwischenpunkten von
![]() .
.
Ist
![]() integrierbar, so gilt
integrierbar, so gilt
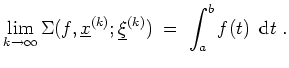
Hauptsatz der Differential- und Integralrechnung.
Für den Hauptsatz gibt es zwei Versionen, je nachdem, ob man von einer zu integrierenden oder von einer abzuleitenden Funktion ausgeht.
1. Sei
![]() ein Intervall, und sei
ein Intervall, und sei
![]() stetig differenzierbar. Dann ist
stetig differenzierbar. Dann ist
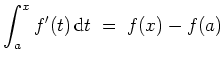
Diese Tatsache wird in der Regel zur Berechnung eines Integrals herangezogen. Man nennt
![]() eine Stammfunktion oder
Aufleitung von
eine Stammfunktion oder
Aufleitung von
![]() . Dies wird auch durch das unbestimmte Integral ausgedrückt, geschrieben
. Dies wird auch durch das unbestimmte Integral ausgedrückt, geschrieben
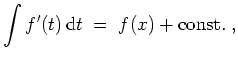
Man schreibt für gegebene Integrationsgrenzen
![]() in einer Rechnung dann auch
in einer Rechnung dann auch
![$ \mbox{$\displaystyle
\int_a^b f'(t)\, {\mbox{d}}t \; =\; [f(x)]_a^b \; =\; f(b) - f(a)\; .
$}$](/inhalt/aussage/aussage1165/img31.png)
2. Sei
![]() ein Intervall, und sei
ein Intervall, und sei
![]() stetig. Sei
stetig. Sei
![]() . Dann ist
. Dann ist
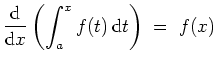
Komplexwertige Integrale.
Sei
![]() eine stetige komplexwertige Funktion, sei
eine stetige komplexwertige Funktion, sei
![]() ihr Realteil und sei
ihr Realteil und sei
![]() ihr Imaginärteil, also
ihr Imaginärteil, also
![]() . Dann setzt man
. Dann setzt man
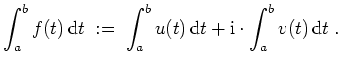
Elementare Regeln.
Sei
![]() ein Intervall, seien
ein Intervall, seien
![]() , seien
, seien
![]() integrierbar auf Teilmengen der Form
integrierbar auf Teilmengen der Form
![]() (erfüllt, falls stetig auf
(erfüllt, falls stetig auf
![]() ), und seien
), und seien
![]() . Es gelten folgende Regeln.
. Es gelten folgende Regeln.
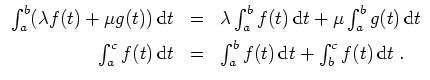
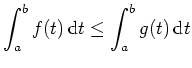
| automatisch erstellt am 18.6.2004 |